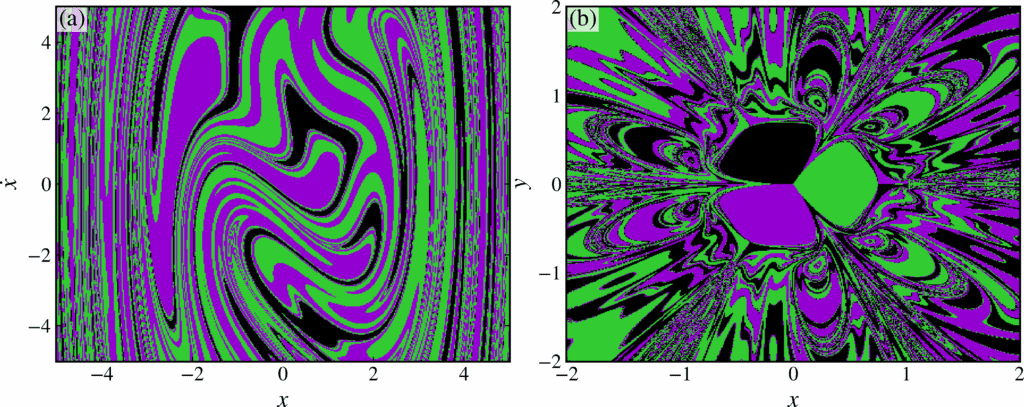
Pesquisadores desenvolveram um módulo de código aberto em Python que promete facilitar a análise de sistemas dinâmicos, tanto contínuos quanto discretos. É o que revela o artigo científico “A Python toolkit for the analysis of dynamical systems”, publicado na revista Chaos, Solitons & Fractals. O estudo apresenta o pynamicalsys, uma ferramenta que reúne em uma única plataforma métodos para simular e quantificar o comportamento de sistemas não lineares, incluindo trajetórias, diagramas de bifurcação, seções de Poincaré, cálculo de expoentes de Lyapunov e outros indicadores de caos.
O objetivo é oferecer uma alternativa simples, acessível e eficiente para o estudo da teoria do caos, com foco em desempenho, reprodutibilidade e uso educacional. O artigo tem a participação de pesquisadores da Unesp, da USP e de instituições estrangeiras: cientistas Matheus Rolim Sales, Leonardo Costa de Souza, Daniel Borin, Michele Mugnaine, José Danilo Szezech, Ricardo Luiz Viana, Iberê Luiz Caldas, Edson Denis Leonel, Chris G. Antonopoulos.
Python é uma linguagem de programação criada no início dos anos 1990 por Guido van Rossum. Ela é conhecida por ser simples, legível e versátil, usada tanto por iniciantes quanto por profissionais. Permite desenvolver sites, programas, jogos, sistemas de automação, inteligência artificial e análise de dados científicos. É uma das linguagens mais populares do mundo porque tem código aberto, funciona em qualquer sistema operacional e possui bibliotecas prontas que facilitam tarefas complexas, como cálculos matemáticos, gráficos e simulações.
O artigo científico situa a criação do módulo no contexto histórico da teoria dos sistemas dinâmicos, que teve início com as ideias de Newton e Laplace sobre um universo determinista. Essa visão foi abalada no fim do século XIX, quando Henri Poincaré mostrou que o movimento de apenas três corpos sob a ação da gravidade não podia ser previsto de forma exata. O problema dos “três corpos” revelou que pequenas variações nas condições iniciais podem produzir trajetórias completamente diferentes, comportamento que hoje se reconhece como caótico.
Décadas mais tarde, Edward Lorenz confirmou experimentalmente essa sensibilidade ao estudar um modelo simplificado do clima. Em 1963, ele mostrou que um sistema de três equações diferenciais podia gerar padrões que nunca se repetiam, embora seguissem leis determinísticas. O resultado foi o primeiro exemplo de um atrator estranho, uma estrutura geométrica que traduz o comportamento caótico em termos matemáticos. A partir desse momento, o estudo do caos se consolidou como um campo interdisciplinar, com aplicações em áreas como física, biologia, economia, meteorologia e ciência da computação.
O pynamicalsys foi criado para auxiliar pesquisadores e estudantes que desejam explorar esse tipo de fenômeno. O módulo implementa recursos para analisar trajetórias, construir diagramas de bifurcação, calcular expoentes de Lyapunov e identificar comportamentos periódicos ou caóticos. Também oferece ferramentas para detectar órbitas periódicas, calcular manifolds invariantes e analisar bacias de atração e regiões de escape, que mostram como diferentes condições iniciais influenciam a evolução de um sistema.
Apesar de ser escrito inteiramente em Python, o pynamicalsys alcança alto desempenho por meio da integração com o Numba, uma tecnologia que acelera os cálculos em até 130 vezes em comparação com a execução pura da linguagem. Os autores explicam que todas as operações usam precisão dupla (float64), o que garante resultados estáveis e minimiza o efeito do ruído numérico. As classes do módulo incluem modelos prontos para uso, mas também permitem criar novas equações de forma simples, o que torna o pacote adequado tanto para pesquisa quanto para ensino.
Além do software em si, o estudo traz uma revisão dos principais métodos usados na análise de sistemas dinâmicos e oferece um guia matemático e computacional detalhado. A documentação completa e os notebooks Jupyter com os códigos utilizados estão disponíveis publicamente, reforçando a proposta de tornar a pesquisa em dinâmica não linear mais acessível e reprodutível. Os autores destacam que, embora exista uma tendência crescente de compartilhar dados e códigos, ainda há resistência em parte da comunidade científica, o que contribui para dificuldades na reprodução de resultados.
O artigo também compara o pynamicalsys com outras ferramentas conhecidas. Diferente do MATCONT, que funciona em ambiente MATLAB e se concentra em métodos avançados de continuação, o novo módulo é totalmente aberto e voltado à comunidade Python. Em relação ao DynamicalSystems.jl, desenvolvido na linguagem Julia, o pynamicalsys se dirige ao público de pesquisadores que já usam Python em outras aplicações científicas. O pacote também difere do JITCode, que é especializado apenas na integração rápida de equações diferenciais. O objetivo, segundo o estudo, é combinar flexibilidade, desempenho e facilidade de uso em um só ambiente, reunindo simulação de trajetórias, análise de bifurcações e detecção de caos.
O trabalho menciona ainda que os pesquisadores planejam integrar o JITCode à classe de sistemas contínuos, o que deve aumentar a eficiência das simulações. Outros projetos semelhantes são citados, como o PyDSTool, o PyChaos, o ChaosPy e o PyAuto, mas o pynamicalsys se diferencia por oferecer um conjunto de funções unificadas com base nas bibliotecas NumPy e Numba. O artigo conclui que a ferramenta pode apoiar tanto o ensino quanto a pesquisa em dinâmica não linear, aproximando o estudo do caos de um público mais amplo, ao mesmo tempo em que mantém rigor matemático e alto desempenho computacional.
(SBF)