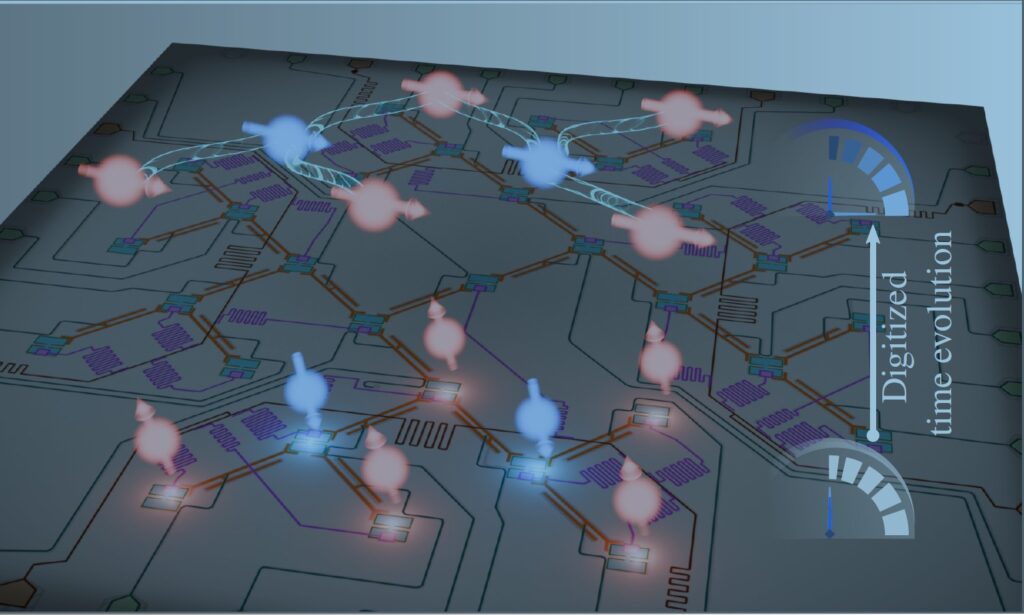
O físico brasileiro Alan C. Santos participou de uma importante pesquisa que demonstrou, pela primeira vez, que é possível simular digitalmente, em temperatura zero, a chamada quebra espontânea de simetria em uma rede de qubits supercondutores, revela o artigo “Digital simulation of zero-temperature spontaneous symmetry breaking in a superconducting lattice processor”, publicado na revista Nature Communications, em parceria com cientistas da China e Dinamarca.
À época da elaboração do artigo, Santos era pós-doutor na Universidade Federal de São Carlos (UFSCar), mas hoje é pesquisador no Instituto de Física Fundamental do Consejo Superior de Investigaciones Cientificas (IFF-CSIC), em Madri (Espanha), financiado pelo programa César Nombela, da Comunidade de Madri, “um programa semelhante ao Jovem Pesquisador da FAPESP”, explica o cientista.
“Recentemente, iniciei meu próprio grupo de pesquisa, atualmente com dois doutorandos, funcionando como um subgrupo do ‘Quantum Information and Foundations Group (QUINFOG)’ do IFF-CSIC. Ainda estamos na fase inicial, mas já atuamos de forma independente em projetos de informação quântica. Então, ainda é um grupo considerado ‘júnior’ nesse aspecto”, explica o cientista, em entrevista por e-mail ao Boletim SBF. “Em poucas palavras, podemos dizer que o CSIC é para a Espanha, o que o CBPF é para o Brasil. Mas na época do início da pesquisa que gerou o trabalho, eu trabalhava na UFSCar com bolsa de Pós-Doutorado da FAPESP.”

Mas o que significa exatamente “quebra espontânea de simetria” e por que é tão importante conseguir simular esse fenômeno a temperatura zero em um sistema quântico digitalizado? Leia a entrevista com o cientista para conhecer mais sobre esse artigo:
Por que é tão importante conseguir simular a quebra espontânea de simetria a temperatura zero em um sistema quântico digitalizado?
A quebra espontânea de simetria ocorre quando, mesmo que as leis que regem um sistema sejam simétricas, o estado fundamental — isto é, sua configuração de menor energia — não respeita essa simetria. Em outras palavras, sob certas condições, o sistema evolui para um estado que rompe espontaneamente a simetria presente nas equações que o descrevem e regem sua dinâmica. Esse fenômeno é fundamental em diversas áreas da física. Na física de partículas, por exemplo, a quebra espontânea de simetria é essencial para o mecanismo de Higgs, que explica por que certas partículas fundamentais possuem massa enquanto outras permanecem sem massa. Em sistemas de matéria condensada, a quebra espontânea de simetria está na base de fenômenos como a supercondutividade e as transições de fase quânticas.
Simular esse fenômeno a temperatura zero é particularmente relevante porque é nesse limite que muitas transições de fase puramente quânticas ocorrem. No entanto, há um obstáculo fundamental: a Terceira Lei da Termodinâmica nos impede de atingir exatamente o zero absoluto de temperatura em qualquer sistema físico real — incluindo computadores analógicos. Isso limita nossa capacidade de estudar diretamente a física que emerge nesse regime.
Por outro lado, em um computador quântico digitalizado, esse limite pode ser superado de forma simulada. Como conhecemos perfeitamente as equações que regem a dinâmica de um sistema quântico e como ele evoluiria se estivesse exatamente a zero Kelvin, podemos simular essa evolução digitalmente, passo a passo, em um processador quântico. Isso abre a possibilidade de explorar com alta precisão a física de baixa temperatura e os mecanismos de quebra espontânea de simetria em regimes inacessíveis experimentalmente com sistemas analógicos.
O artigo mostra uma transição de fase de um estado antiferromagnético clássico para um estado ferromagnético quântico. Como essa transição foi observada no experimento e o que ela nos revela sobre os limites, ou talvez as novas possibilidades, da física conhecida até agora?
Tanto na abordagem teórica quanto no experimento, a natureza quântica do estado ferromagnético foi caracterizada por meio da emergência de emaranhamento no sistema. Como o emaranhamento é um tipo de correlação genuinamente quântica — sem equivalente clássico —, conclui-se que o sistema realiza uma transição de um estado antiferromagnético clássico — sem emaranhamento — para um estado ferromagnético quântico, distinto de um estado ferromagneto clássico, que também não apresenta emaranhamento.
Para testemunhar a presença de emaranhamento, calcula-se teoricamente a entropia de Rényi entre diferentes partes do sistema. A complexidade surge na implementação experimental dessa medida, pois o cálculo exige a chamada tomografia de estados quânticos, que se torna extremamente desafiadora à medida que o número de qubits aumenta — sendo que sistemas com apenas 7 spins já são considerados relativamente grandes para esse tipo de abordagem. Assim, técnicas experimentais baseadas em medições aleatórias foram utilizadas para estimar a entropia de Rényi do sistema, permitindo assim confirmar a presença de emaranhamento quântico.
Nossos resultados abrem caminho para novas pesquisas em duas frentes principais: (1) matéria condensada e transições de fase, e (2) simulação quântica de sistemas de muitos corpos. No contexto das transições de fase, é muito bem documentado transições de fase que acontecem em sistemas com interação de longo alcance e com temperatura diferente de zero. Por exemplo, sabemos que, sem interações de longo alcance, é impossível obter certas transições de fase em sistemas com temperatura diferente de zero. No nosso trabalho, a gente tenta levantar questões sobre quais tipos de transições de fase quântica podem ser acessadas em sistemas com interações restritas a primeiros vizinhos, mesmo que para isso tenhamos que manter ou simular temperatura zero. Já na área de simulação quântica, permanece a dúvida sobre a escalabilidade do método: seria possível aperfeiçoá-lo para lidar com sistemas maiores e mais complexos? Isso dependerá, em grande parte, da nossa capacidade de implementar a digitalização de forma eficiente.
Um dos pontos centrais do estudo foi o uso da chamada “evolução adiabática digitalizada” (DAE). Poderia nos explicar, de forma simples, o que é essa técnica e por que ela representa um avanço em relação a outras formas de simulação quântica, como o Quantum Approximate Optimization Algorithm (QAOA)?
Essa ideia de digitalizar a evolução adiabática nasce da necessidade de implementar evoluções adiabáticas — que usam campos que variam continuamente no tempo e são nativas da computação analógica — em computadores digitais, onde essa continuidade na mudança de parâmetros não é possível. Assim, o que fazemos é quebrar a dinâmica em intervalos de tempo discretos e aplicar pulsos para simular a dinâmica, enquanto monitoramos se o sistema segue a trajetória desejada. Como analogia, seria como se um filme de 10 minutos mostrando o movimento de um barco no mar precisasse ser resumido em 10 fotos, cada uma mostrando a posição do barco e o comportamento do mar. Você ainda seria capaz de contar a história do barco e das ondas, mas de forma discretizada. Ou seja, temos uma imagem do barco a cada 1 minuto e podemos verificar se ele está seguindo o caminho certo.
A vantagem desse método, em comparação com outras formas de simulação, como o QAOA, depende muito do objetivo da aplicação. Por exemplo, ao compararmos com computadores analógicos, a vantagem é clara: certas dinâmicas não podem ser implementadas em computadores analógicos por limitações técnicas ou mesmo por princípios fundamentais (como mencionado anteriormente). No entanto, a comparação com outros métodos digitalizados ainda não apresenta uma vantagem definitiva. Podemos, sim, mencionar alguns pontos positivos. Por exemplo, nossa proposta não requer nenhuma integração com computadores ou otimizadores clássicos, como no caso do QAOA. Utilizamos apenas as informações já contidas no sistema para digitalizar a dinâmica e obter os resultados. Por outro lado, ainda comparando com o QAOA, para algumas tarefas específicas nosso método pode exigir mais recursos, justamente por não fazer uso de otimização. No entanto, o QAOA demanda um custo adicional de integração com computadores clássicos, o que pode ser um limitante em certos cenários.
Em resumo, esses métodos têm vantagens e desvantagens, e tudo depende do problema em questão e dos recursos disponíveis. Por exemplo, se otimizadores clássicos não estão disponíveis ou são ineficientes para um dado problema, o QAOA perde sentido e nosso modelo se torna mais vantajoso. Na verdade, eu diria — ainda que por especulação — que não será fácil encontrar um modelo que seja superior a todos os outros em todos os aspectos. Sinto que há ainda um grande trabalho pela frente até que possamos dar uma resposta definitiva a essa questão.
O trabalho também discute o papel do emaranhamento quântico e da entropia de Rényi. Como esses conceitos ajudam a identificar que a simulação foi bem-sucedida e que, de fato, ocorreu um comportamento quântico real no sistema?
A entropia de Rényi é utilizada como testemunha de emaranhamento. Quando essa medida satisfaz certos critérios — discutidos brevemente no artigo — é possível afirmar com segurança a presença de emaranhamento no sistema. Mesmo com a presença de ruído experimental, um dos principais desafios em algumas plataformas de computação quântica, foi possível medir valores da entropia de Rényi acima do limiar necessário para caracterizar o emaranhamento. Isso, por si só, já comprova o caráter quântico da dinâmica observada.
A entropia de Rényi, portanto, permite detectar o emaranhamento nas fases ferromagnética e antiferromagnética ao final de cada evolução digitalizada. E o emaranhamento, por sua vez, é uma assinatura inequívoca da natureza quântica do estado final — algo que não seria possível observar sem o comportamento coletivo e quântico do sistema.
O senhor vê esse tipo de simulação sendo usado no futuro para resolver problemas fora da física fundamental, como em otimização, inteligência artificial ou modelagem de sistemas complexos?
Na computação quântica, é plausível imaginar cenários em que evoluções adiabáticas digitalizadas desempenham um papel relevante. O núcleo dessa proposta está na combinação de duas ferramentas poderosas: (1) evoluções adiabáticas, úteis em problemas de otimização, e (2) computação quântica baseada em portas lógicas — ou “computação digitalizada” como venho me referindo — que é universal e compatível com técnicas como correção de erros.
O objetivo é unir o melhor dos dois mundos: aproveitar o poder das evoluções adiabáticas para otimização, mas dentro do framework robusto da computação digital quântica. Caso dispositivos quânticos eficientes sejam desenvolvidos, esse modelo pode ter grande potencial, inclusive em áreas emergentes como o Quantum Machine Learning, a versão quântica do aprendizado de máquina clássico.
No entanto, é preciso cautela ao promover qualquer proposta em computação quântica. Apesar do potencial teórico comprovado, a tecnologia ainda está em um estágio muito inicial. Para avançar, são necessários mais investimentos em infraestrutura, formação de pesquisadores e desenvolvimento tecnológico — especialmente em países ainda fora do mapa da inovação quântica. O Brasil é um exemplo claro: precisa investir, mas, acima de tudo, investir com estratégia. O segredo não está apenas no quanto se investe, mas em como e onde devemos investir.
(Colaborou Roger Marzochi)